以下の問題に答えてください。
プレーヤーの前に閉じた3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。
プレーヤーは新車のドアを当てると新車がもらえる。
プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。
ここでプレーヤーはドアを変更すべきだろうか?
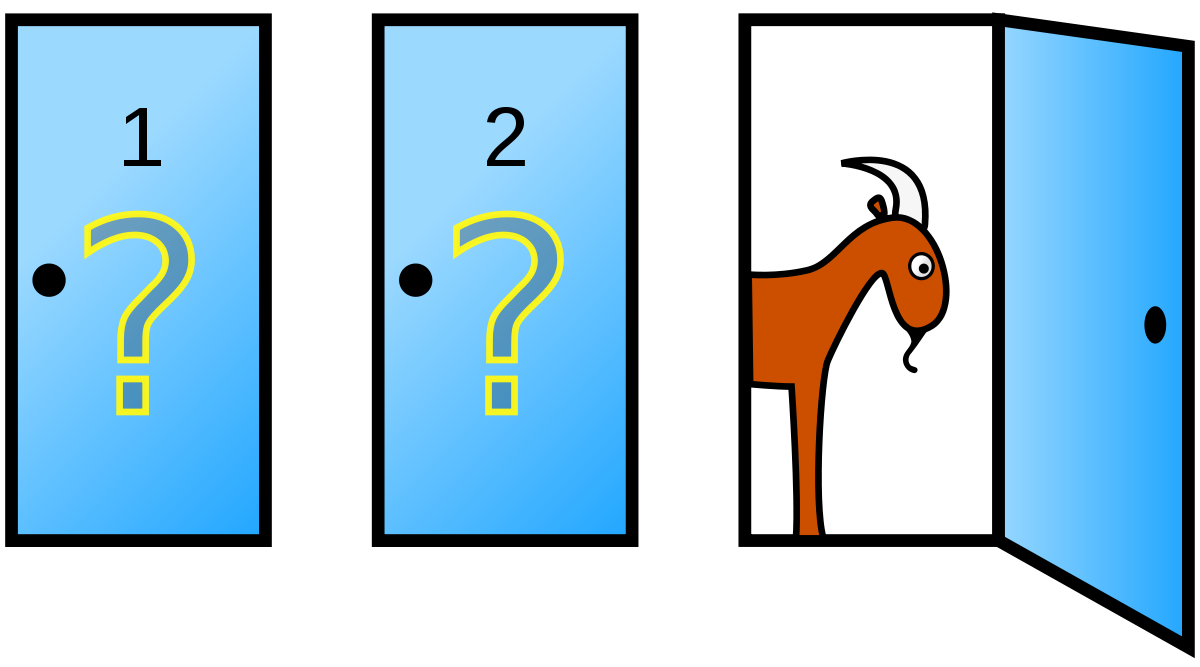
これは有名なモンティ・ホール問題という確率論の問題です。
最初の条件では、ドアが3つで、景品が1つなので、当たる確率は1/3ですね。
それでは、選んだドアを変えなかった場合、当たる確率は何パーセントでしょうか。
直感的には「残る2つのドアの当たる確率はそれぞれ1/2になる」「変えても変えなくても当たる可能性は変わらないので、変えない」と感じることが多いと思います。
しかし、それは不正解です。
これは、後に「モンティ・ホール問題」と、名の付くほど有名な問題で、当時はアメリカの、数学者や経済学者でも意見が分かれ、大論争になりました。
頭が良ければ良いほど、残るドアは2つで、当たる確率は等しいのだから、どちらも2分の1と考えたくなります。
また、人間の本能的にも「変えても良い」と言われると、ひっかけのようで変えたくなくなりますよね。
この問題の正解は、
「最初に選んだドアから変えた方が当たる確率はあがる」
その確率は、「そのまま開ければ当たる確率は3分の1、ドアを変えれば3分の2の確率で当たる」である。
となります。
納得いった方もいれば、納得いかない方もいると思います。
納得いかない方は、ぜひ、wikipediaの解説をお読みください。
この問題は数字を扱うとても楽しい問題です。これからの時代はSTEM教育が必須の時代。数学は外せない学問です。
このような問題が出た時に「確率って面白い」「この問題の条件のキモは何だろう?」と興味関心を持てる子を育てたいですね。